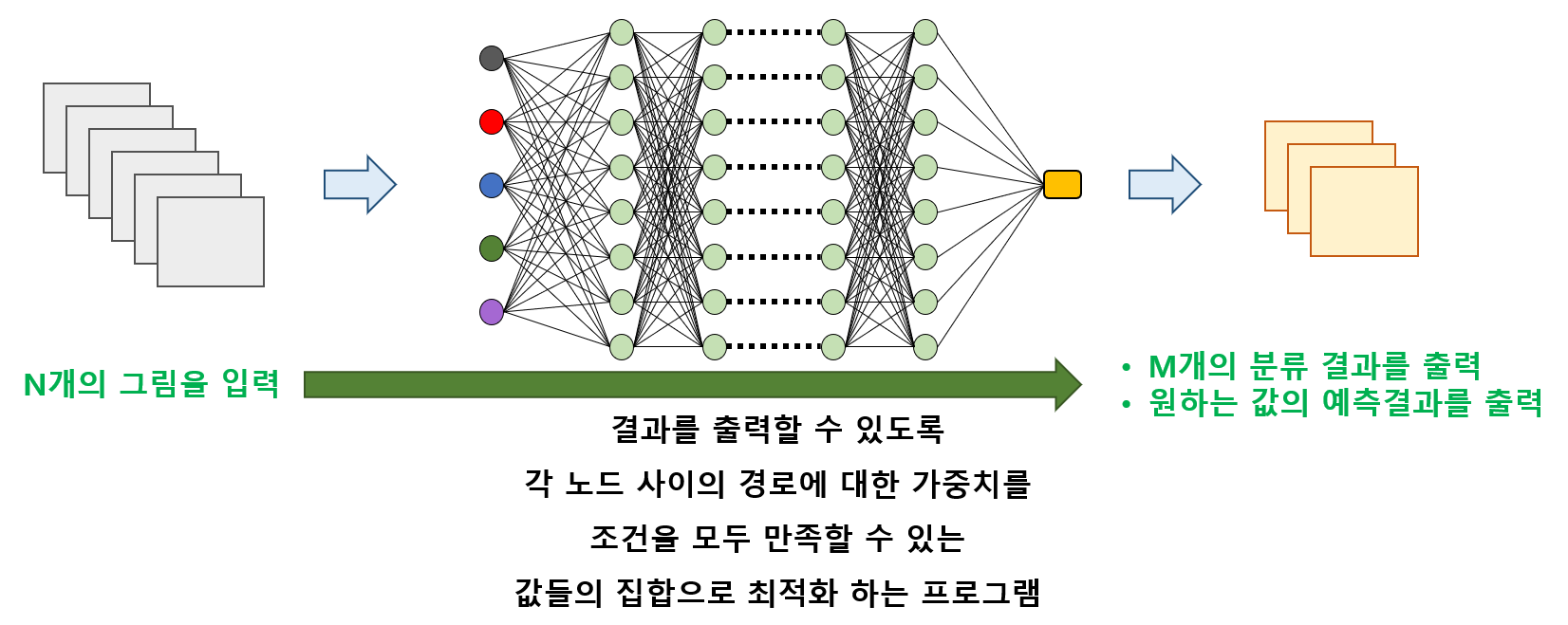
Deep Learning 개요

1. 딥러닝이란 무엇인가?

  • 기본적인 딥러닝의 개념
    • 인공지능의 한 분야
    • 인공신경망을 기반으로 한 기계 학습 기법
    • 인간의 뇌에서 영감을 받은 다층 구조의 심층 신경망을 사용하여 대량의 데이터로부터 자동으로 복잡한 패턴을 학습하고 예측함
    • 딥러닝의 핵심은 ‘특징 추출’의 자동화
    • 전통적인 머신러닝과 달리 수작업으로 특징을 정의할 필요 없이 데이터로부터 스스로 학습함
    • 이를 통해 이미지 인식, 자연어 처리, 음성 인식 등 다양한 분야에서 뛰어난 성능을 보여주고 있음


  • 인공지능에서 딥러닝의 위치


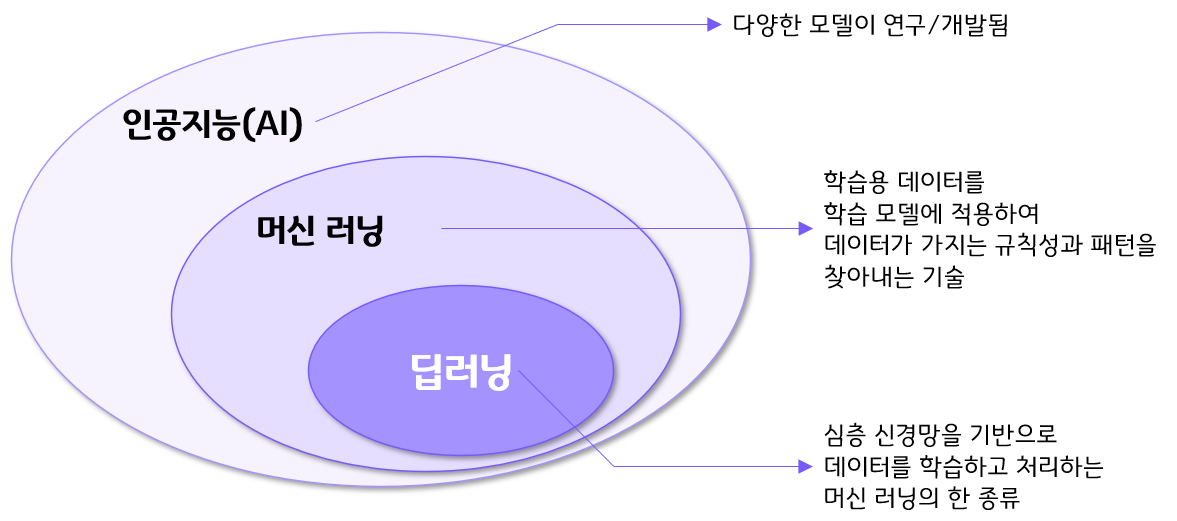
    • 인공지능의 연구 형태는 크게 5가지로 분류함
      • 기호주의: 역연역법 ➜ 규칙기반 전문가 시스템을 중심으로 발전
      • 연결주의: 신경망 모델을 통한 학습 중심으로 발전
      • 진화주의: 유전자 알고리즘을 주축으로 발전
      • 베이즈주의: 베이즈 추론 기반의 통계 모델을 중심으로 발전
      • 유추주의: 사물, 현상에 대한 유추를 기반으로 학습을 진행

    • 기호주의는 암호학, 알고리즘 등 현재의 대부분의 IT 기술의 기반을 담당하게 됨
    • 연결주의는 현재의 딥러닝 기술의 기반
    • “연결주의 + 진화주의 + 베이즈주의 + 유추주의”가 복합적으로 현재의 머신러닝 기술을 구성함

2. 신경망 모델

2.1 신경망 모델이란?

  • 신경세포의 간단하고 효과적인 처리 방식에 착안해 구현된 머신 러닝 모델의 한 종류
  • 신경세포의 형태와 동작을 극도로 단순화 시킨 뉴런 모델을 다수 연결하여 네트워크를 구성
    ➜ 다량의 뉴런(Neuron)들이 층(Layer)으로 연결되어 간단한 계산과 연결 방식을 통해 복잡한 문제를 해결하는 모델
  • 뉴런의 동작 방식은 컴퓨터 프로그램의 방식에 비해 다양한 장점을 지님

2.2 신경망 모델의 아이디어 기반

  • 1943년 워런 맥컬록, 월터 피트의 최초의 신경망 모델이 시초

  • 헵의 규칙이 신경망 모델의 동작을 정의하는 기반이 됨
    • 시냅스의 앞과 뒤에서 동시에 신경세포가 흥분할 때, 해당 시냅스의 효율이 강화됨

2.3 신경세포/신경망의 구조와 작동

  • 신경세포의 구조와 연결 형태

            
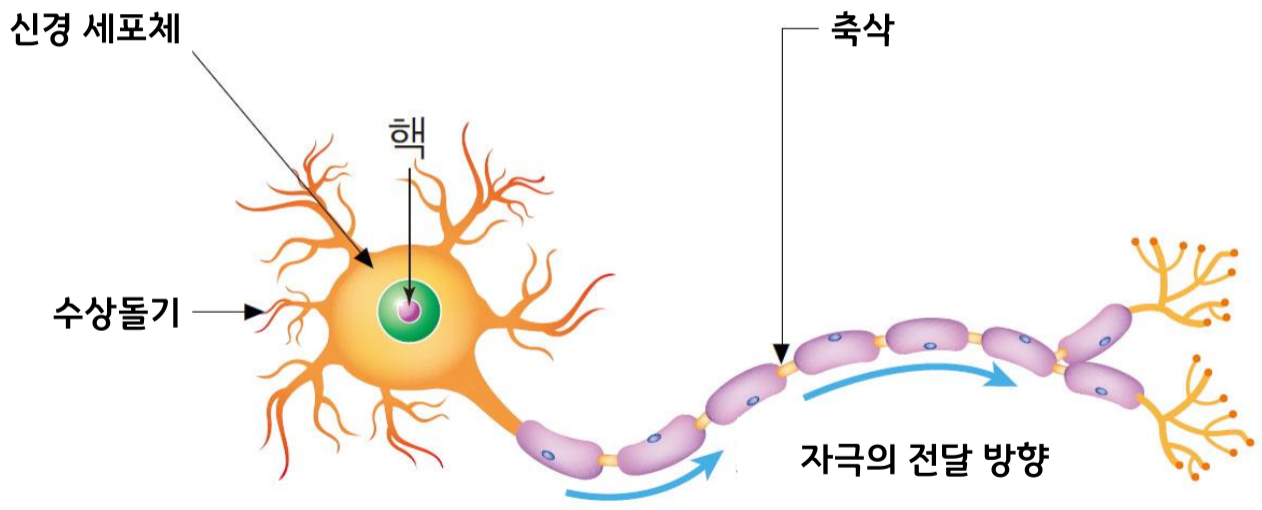
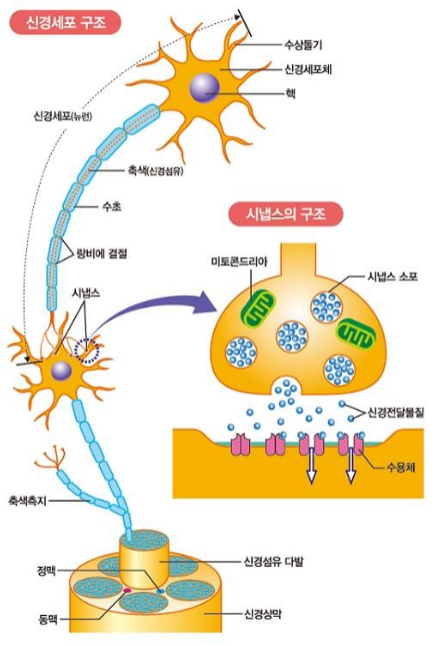
    • 신호의 전달은 전기로 이루어짐
    • 신경세포의 말단에는 시냅스가 존재
    • 시냅스 사이의 신호 전달은 신경전달물질이라는 화학물질을 통해전달됨
    • 신경전달물질
      • 세로토닌, 도파민, 엔돌핀, 아드레날린 등..


  • 신경세포의 신호 처리 과정

    1. 신경체계를 구성하는 수많은 신경세포들
    2. 다양한 감각기관을 통하여 (전기)신호를 발생, 전달
    3. 각 신경세포는 수많은 시냅스를 통해 신호를 전달 받음
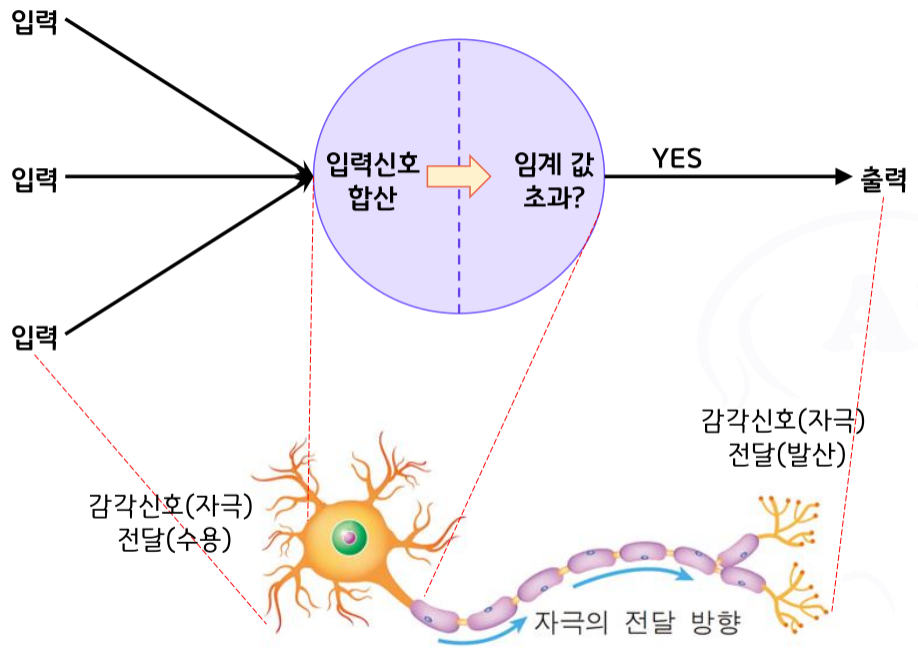
    4. 전달 받은 신호는 대체로 무시하지만.. 동시에 전달된 신호의 합이 임계값을 넘으면 활성화(발산, 흥분한다 라고 표현함)
    5. 활성화 된 신경세포는 활성화 패턴에 따라 신경전달물질 분비
    6. 이웃 신경세포는 신경전달물질을 수용하면서 이온화 작용, 화학작용을 통하여 전기 신호 발생
    7. 처리 단계 반복

2.4 신경세포, 신경망의 모델링

  • 퍼셉트론(Perceptron) 모델
    • 1958년, 심리학자 프랭크 로젠블랫(Frank Rosenblatt)이 개발한 신경망 모델
    • 당시의 인공지능-신경망 모델 중 가장 유명한 모델
    • 1960년, 로젠블랫과 동료들은 퍼셉트론이 유한하게 많은 훈련 주기에서 매개변수가 구현할 수 있는 모든 작업을 학습할 수 있음을 보여줌
    • 퍼셉트론 수렴 정리는 단층 신경망에 대해 입증됨
    • 당시의 신경망 연구는 상당수의 개인이 취한 뇌-기계 문제에 대한 접근 방식이 중심이었음
    • 뉴욕타임즈의 보고서와 로젠블랫의 진술에 따르면 신경망은 곧 이미지를 보고, 체스에서 인간을 이기며 번성할 수 있을 것이라고 주장함
    • 비슷한 시기에 등장한 기호처리 기반의 인공지능 연구 그룹과 자금 및 인력을 놓고 경쟁하게 됨

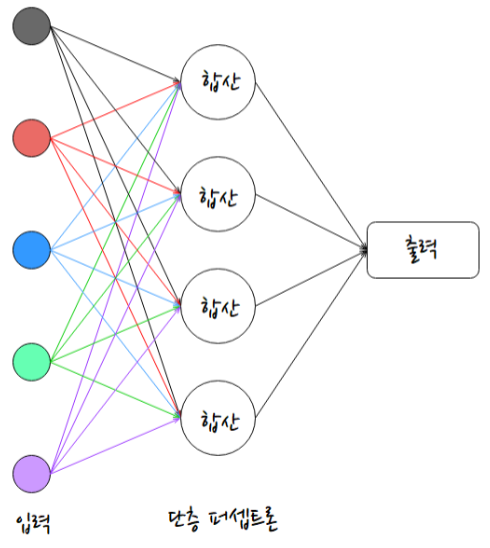
  • 단층 퍼셉트론(Single Layer Perceptron, SLP)
    • 개요
      • 다수의 퍼셉트론이 하나의 층을 이루고 있는 형태
      • 센서 데이터 등 다양한 데이터를 각 퍼셉트론의 입력으로 전달
      • 각 퍼셉트론은 입력된 데이터를 모아서 합산
      • 합산 결과가 임계 값을 넘으면 1, 넘지 않으면 0 출력
      • 입력층에서 각 퍼셉트론으로 진행되는 통로에는 가중치 적용 (가중치는 모든 통로가 각각 다르게 적용될 수 있음)
      • 아래 그림에서 4개의 퍼셉트론이 각각 1, 0, 0, 1 이라는 결과를 낸다면, 최종 출력은 1001 이라는 2진수 값이 나오는 형태

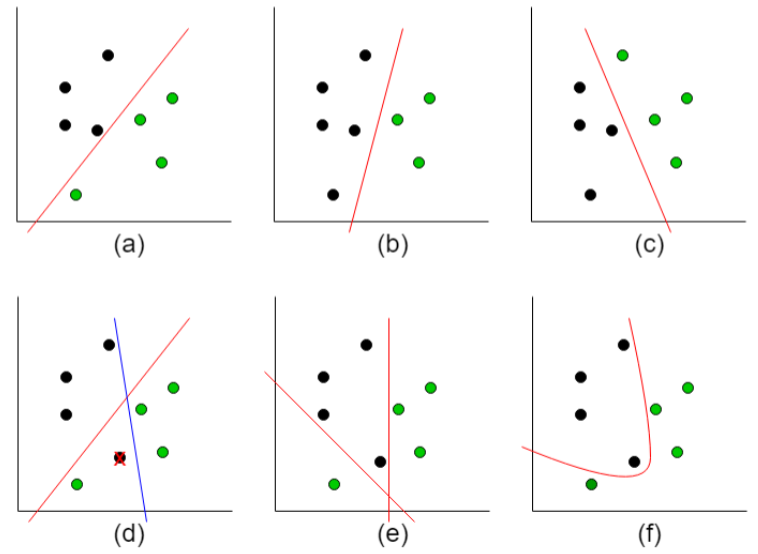
    • 단층 퍼셉트론의 문제점
      • 한 층의 변경가능한 퍼셉트론만 존재
        ➜ 1개의 선을 그어 분리 가능한 패턴만 분류 가능
        ➜ XOR 문제의 원인

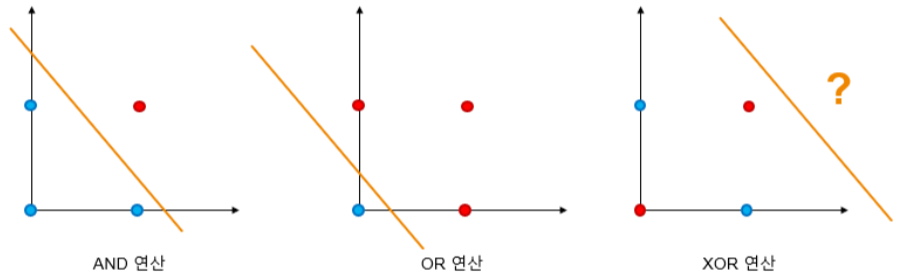
    • XOR 문제
      • MIT의 마빈 민스키(Marvin Minsky), 시모어 패퍼트(Seymour Papert)가 1969년 발표한 논문인 ‘Perceptrons’ 에서 신경망 모델은 XOR 연산과 같은 기본적인 논리문제를 해결할 수 없음을 증명함
        ➜ AI의 겨울(신경망의 겨울, 암흑기)을 이끌어내는 단초가 됨
    • 진짜 문제점
      • 더 큰 문제는 따로 있음
      • 단층 퍼셉트론의 구조를 보면…
      • 가중치를 변경할 수 있는 방법이 없다 → 학습이라는 개념이 없음
      • 한 번 생성된 후에는 아무런 변형이 없는 단순한 분류 알고리즘에 불과함 → AI로서의 능력, 가치가 없음

      • 당시의 신경망 모델은 기계적으로 구성되었기 때문에 각 가중치 업데이트는 전기모터를 이용하여 직접 조정해 주었음
      • 정확하게는 학습을 위한 개념은 연구에서도 도입되었고, Backpropagation이라는 알고리즘도 나왔지만 기술 부족으로 적용하지 못했음

      당시의 신경망 기계


  • XOR 문제의 해결 방안 등장


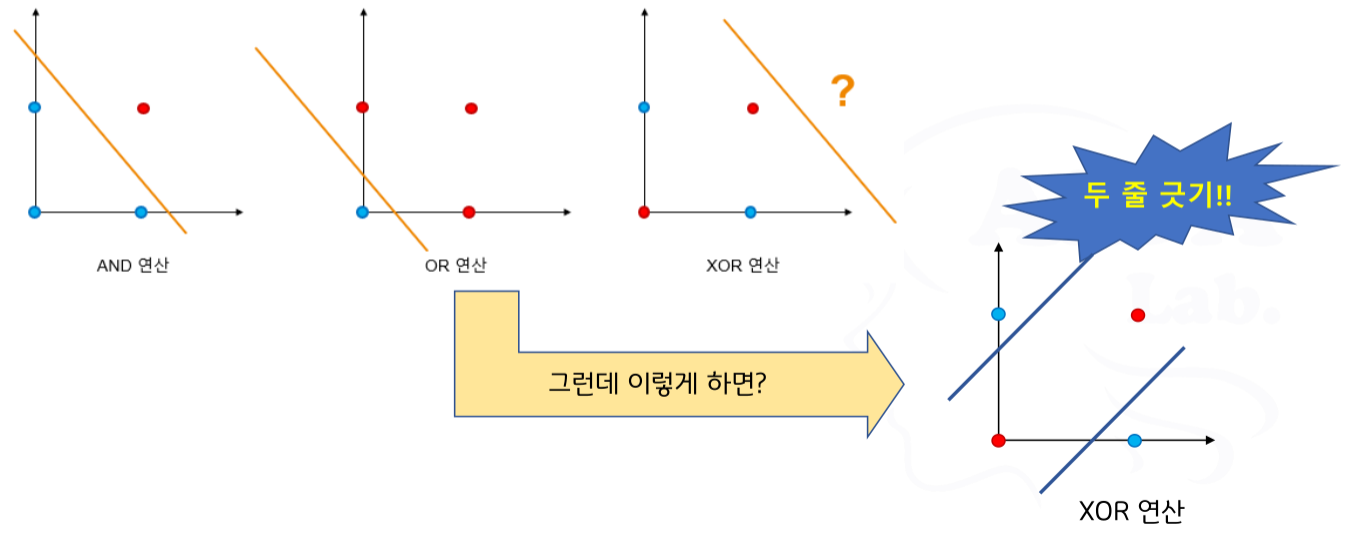
    • 직선의 수를 늘림으로써 다양한 패턴의 분류가 가능해 짐 → XOR 문제의 원인 제거 성공 → 다층 퍼셉트론 등장

    일설에 따르면 ‘Perceptrons’를 발표한 민스키, 패퍼트도 다층 퍼펏셉트론이 XOR 연산을 해결할 수 있음을 알고 있었다고 함


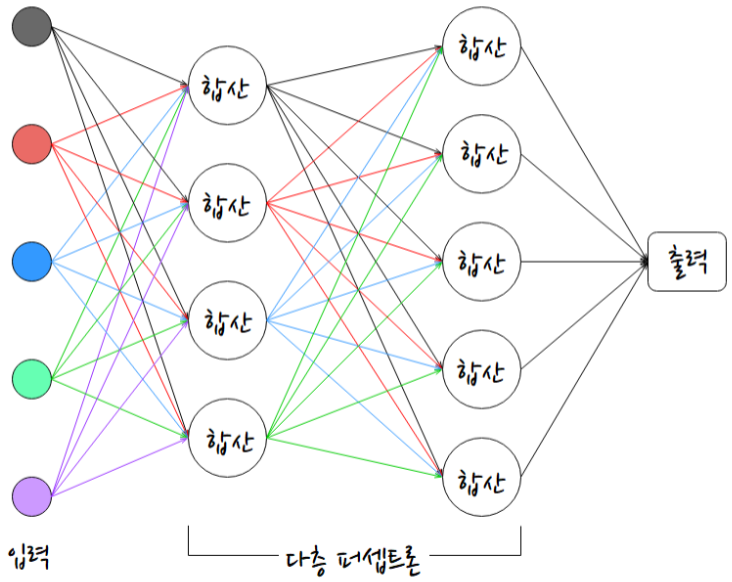
  • 다층 퍼셉트론(Multi Layer Perceptron, MLP)
    • 개요
      • 다수의 퍼셉트론 층이 네트워크를이루는 형태
      • 처리 방식은 단층 퍼셉트론과 동일함

    • 또 문제점
      • 단층 퍼셉트론과 마찬가지로 각 통로의 가중치를 변경할 방법이 없음
      • 한 번 생성되면 변경 불가능한 분류 알고리즘
      • 역시 학습의 개념이 없다 ➜ 인공지능이 아닌 단순한 분류 알고리즘
    • 해결책은?
      • 수행할 때마다 예전 데이터를 들고 와서 가중치를 수정해 주면 어떨까?
      • 그럼 아예 앞뒤로 왔다 갔다 반복하면서 가중치를 바꾸어 주면 어떨까?
      • 이런 생각에 Back Propagation (역전파) 알고리즘이 제안되어 왔으며
        ➜ 1986년 Rumelhartt D. E., Hinton G. E, William R. J.의 “Learning representations by back-propagation errors” 논문에서 적용 성공 발표
    • Backpropagation
      • 라이프니츠 연쇄규칙(Leibniz Chain Rule, 1673)을 네트워크에 효율적으로 적용한 알고리즘
      • 1962년 프랭크 로젠블랫이 ‘Back-propagation Error Correctoin’이라는 용어 자체는 도입했으나 장시간동안 구현 방법을 몰랐음

    • Back Propagation (역전파) 알고리즘





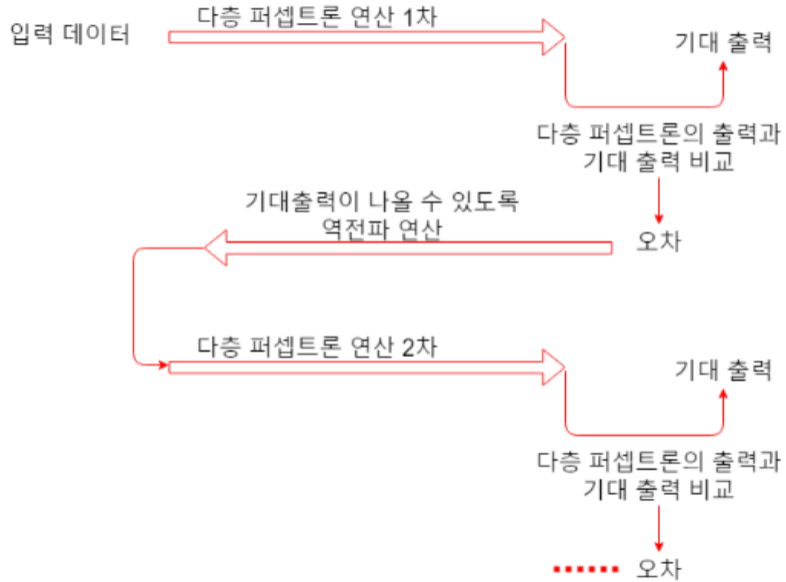
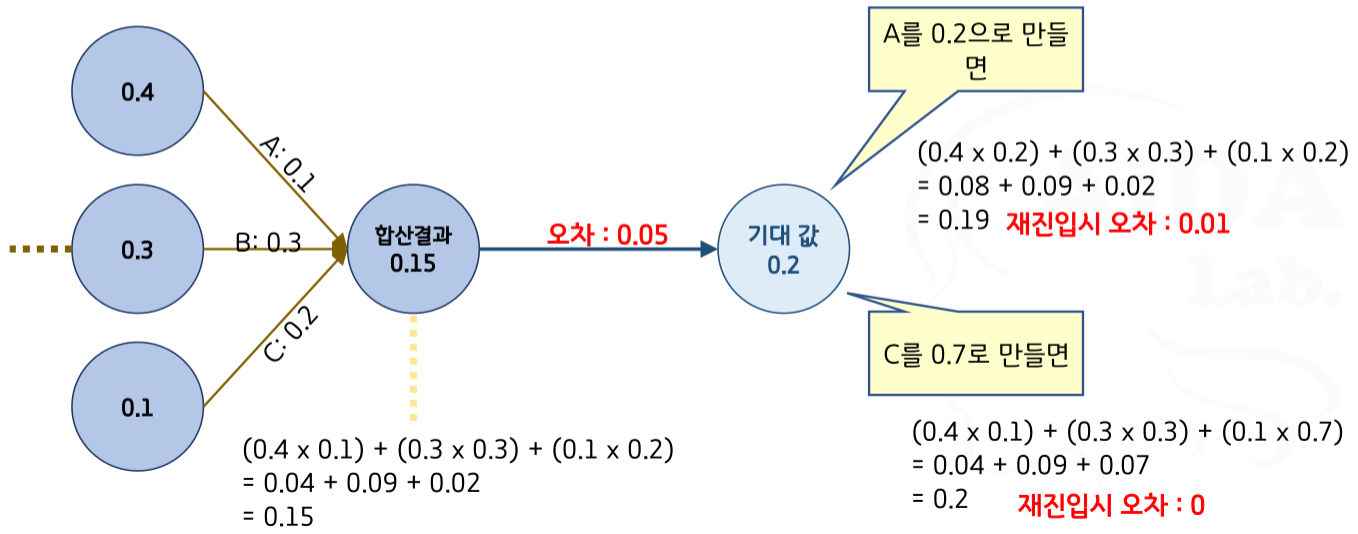
    • 역전파 시 어떻게 가중치를 조절하는가?
      • 조절 내용: 은닉층을 거친 결과값과 기대한 결과값의 오차를 줄이는 방향으로 수정
        • 1단계

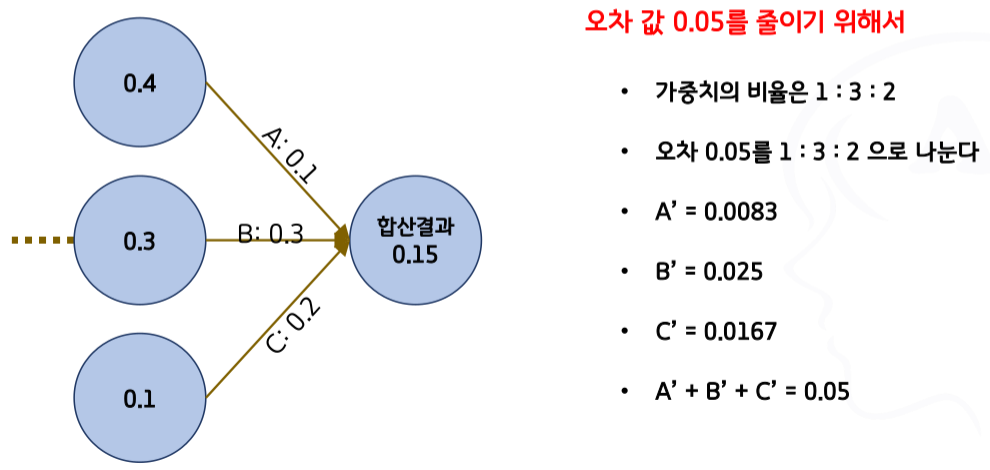
        • 2단계

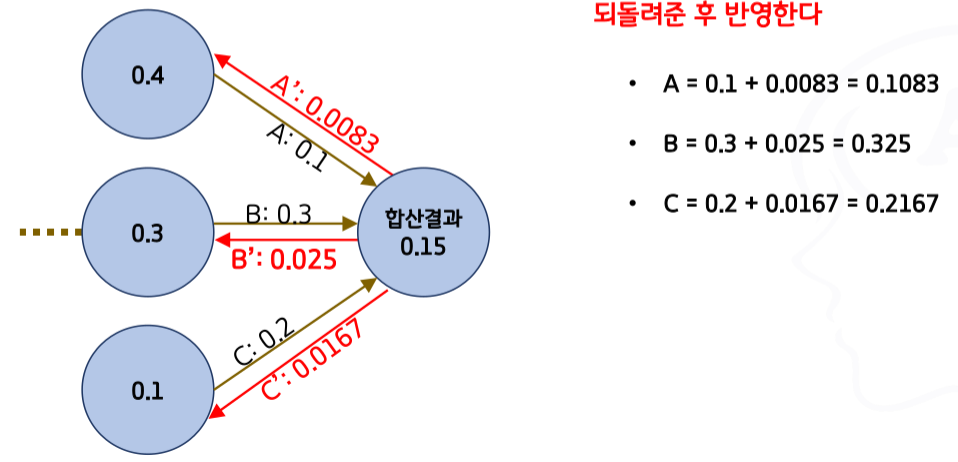
        • 3단계

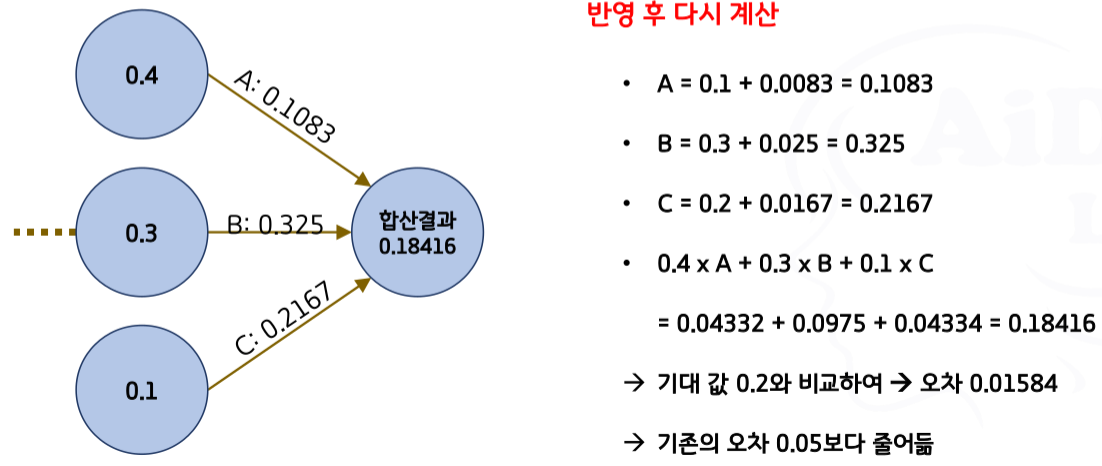
        • 4단계

    • Back Propagation (역전파) 알고리즘을 구현한 다층 신경망에서
      • 그 층을 훨~씬 많이 만들어서 수 많은 분류 작업을 수행할 수 있게 한다면?
      • 다층 신경망(Multilayer Neural Network) ➜ 심층 신경망(Deep Neural Network) 으로 진화
      • 심층 신경망을 이용한 학습 모델 = 딥 러닝(Deep Learning)


2.5 딥러닝 모델

2.5.1 단계별 처리 방식

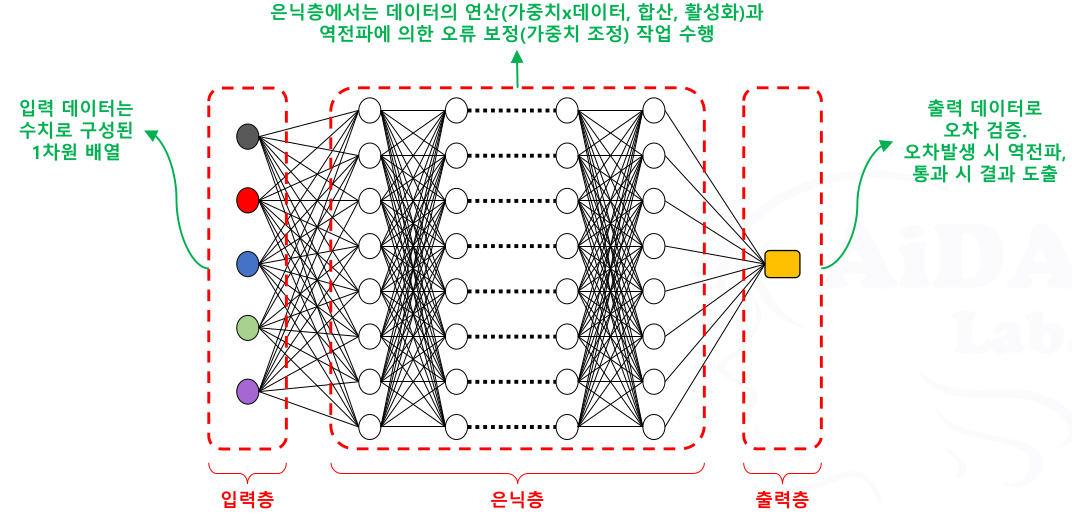
  • 전체 구조


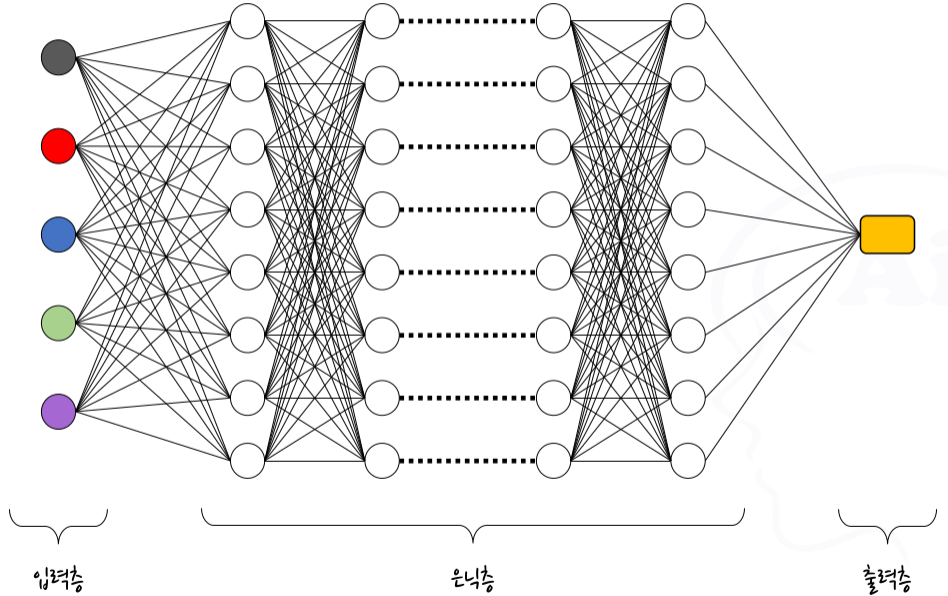
  • 입력층


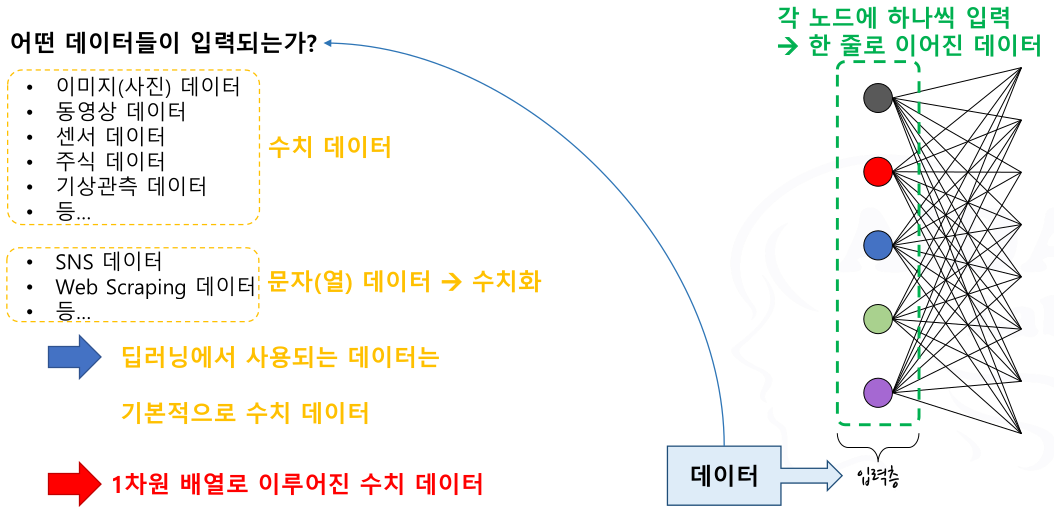
    • 이미지 / 영상 데이터가 왜 수치 데이터인가?

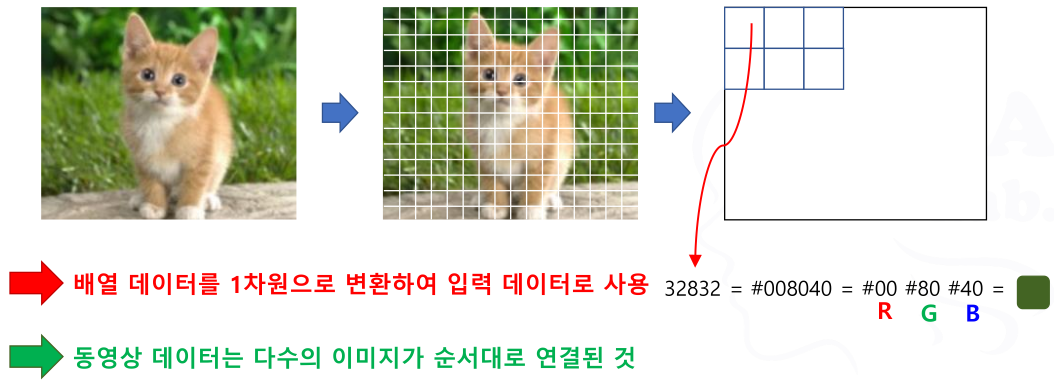
  • 은닉층





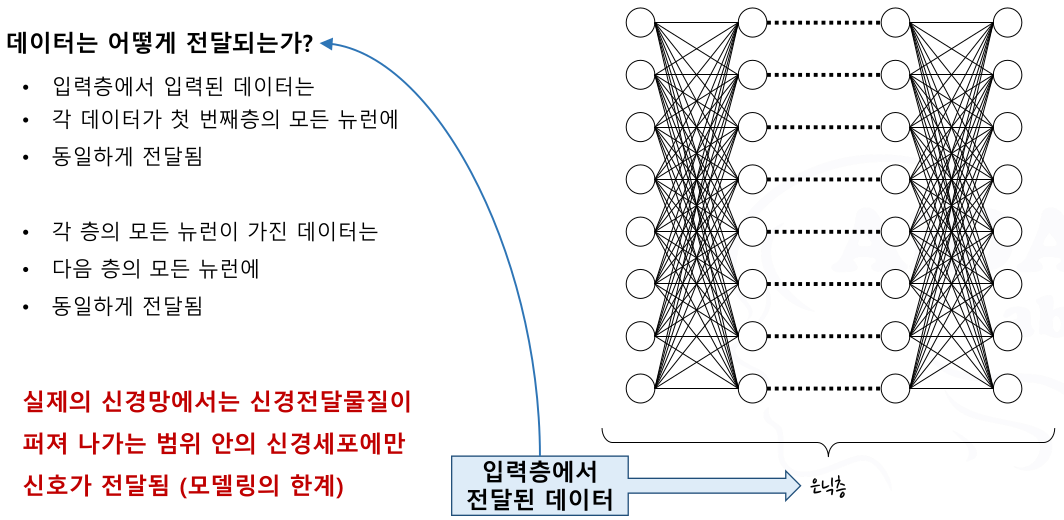
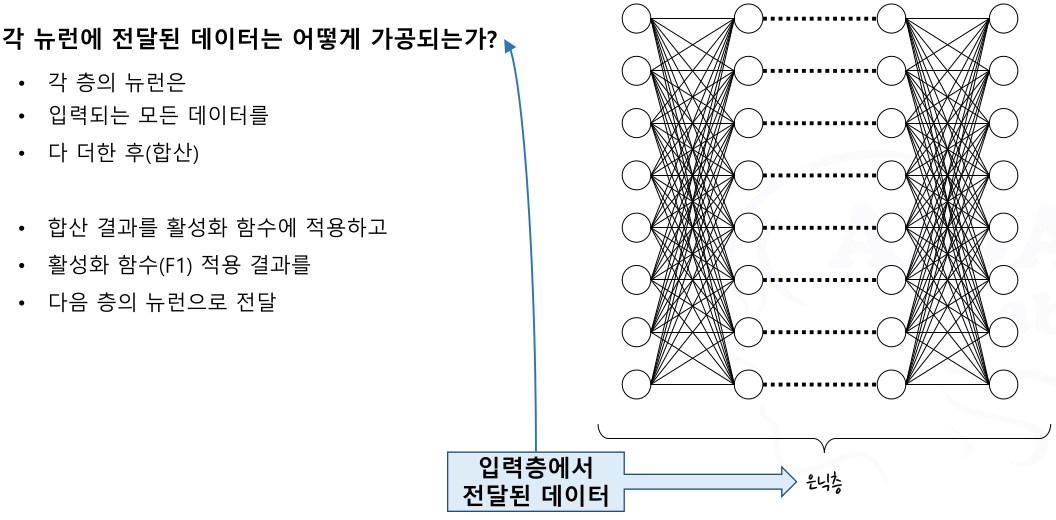
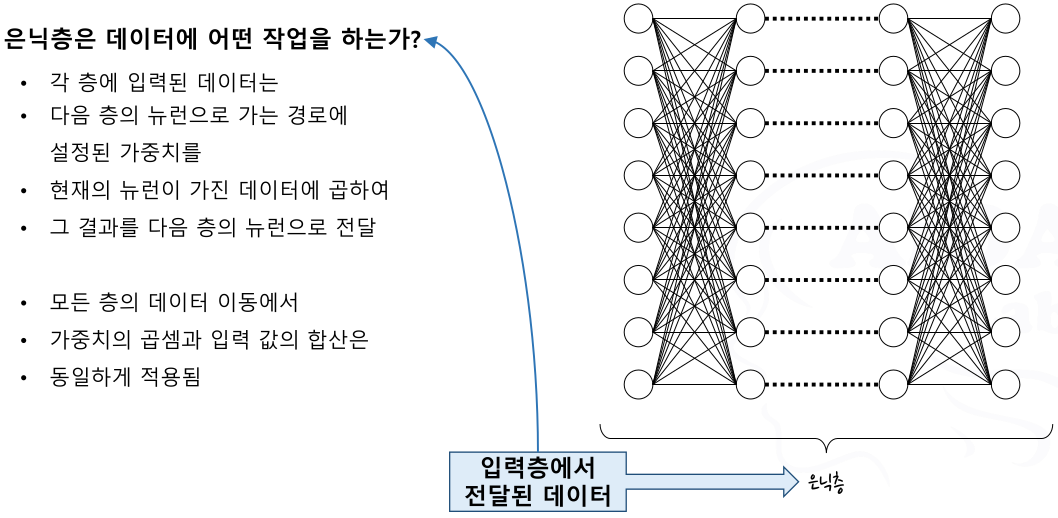
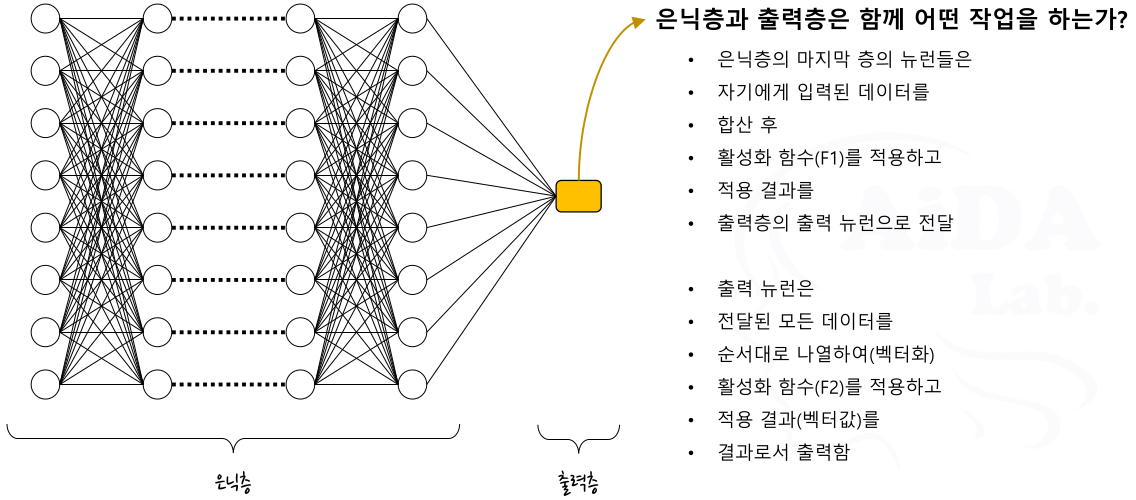
  • 출력층


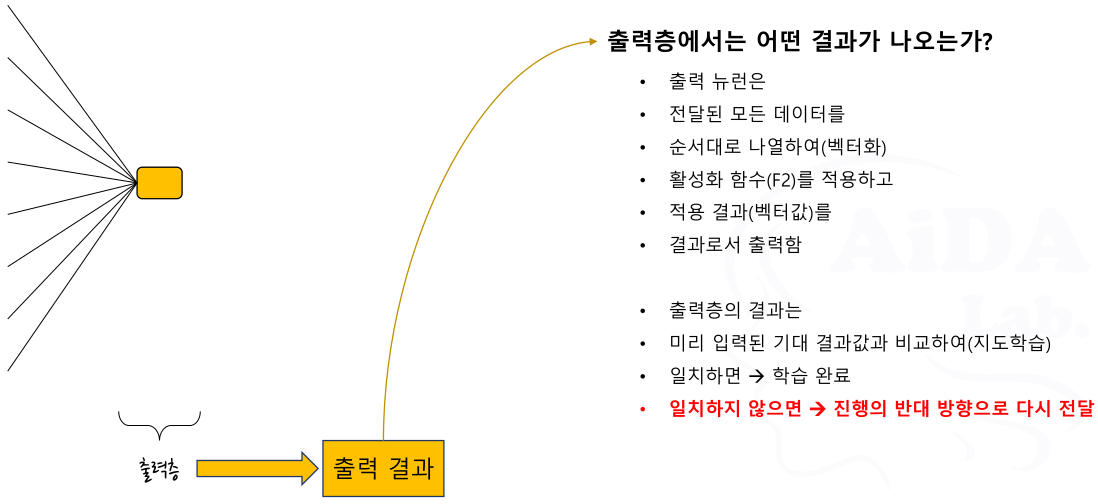
  • 딥러닝 모델의 전체 모습

2.5.2 세부 처리 내용

  • 활성화 함수(Activation Function)
    • 신경망을 구성하는 각 퍼셉트론에서 임계 값을 넘었을 때 출력(활성화)을 처리하는 함수
    • 함수의 정의
      • 입력: 이전 층의 디바이스 또는 퍼셉트론들로부터 전달되는 데이터
      • 함수의 동작: 입력 값의 합산 + 합산결과와 임계 값의 비교 + 출력 결정(활성화 조건)
      • 출력: 퍼셉트론 층의 연산 결과값. 다음 층의 뉴런에 대한 입력 또는 최종 층의 출력
    • 활성화 함수는 왜 필요한가?
      • 생물학적 / 신경과학적 필요성
        • 피부, 눈과 같은 감각기관이 어떤 자극을 받아 신호를 발생시키면
          ➜ 그 신호는 축삭을 통해서 이동하고 → 축삭의 말단에 있는 시냅스를 거쳐 다음 뉴런으로 전달
        • 그런데 전달되는 모든 신호(아주 미세한 신호부터 강한 신호까지)를 모두 다음 뉴런으로 전달한다면?
        • 생활/생존 자체가 어려워지며 매우 비 효율적
        • 우리 몸에서 반응할 필요가 있는 수준까지만 신호를 전달하고 나머지의 신호는 무시한다!! ➜ 진화의 결과
        • 이 기준을 모델에 반영한 것이 활성화 함수
      • 수학적 필요성
        • 입력 데이터는 연속, 선형 데이터이지만 출력 데이터는 이산 데이터(예측 및 분류 등)
          ➜ 선형성을 가진 데이터를 비선형성을 가진 데이터로 변환시킬 필요가 있음
    • 즉, 활성화 함수란..
      • 뉴런의 신호 흐름을 모델링 할 때 각각의 뉴런에 제한을 걸어 둔 것
      • 활성화 함수에서 적용한 기준에 따라 조건을 만족하는 경우에만 다음 뉴런으로 신호를 전달하기 위한 것
    • 그럼 활성화 함수는 왜 그렇게 많은 형태가 존재하는가?
      • 우리는 아직 우리의 뇌와 신경들이 어떻게 동작하고 서로 어우러지는지 정확하게 알지 못함
      • 따라서 우리가 AI로 해결하고자 하는 문제에 맞게 가장 효율적이고 적절한 활성화 함수를 계속 연구, 개발하여 활용하는 것
    • 활성화 함수의 조건
      • 정의역(함수에 입력 가능한 값의 범위, 집합) 안에서 연속이며 무한해야 한다
      • 단조 함수여야 한다 (방향을 바꾸지 않아야 한다)
      • 비선형 함수여야 한다.
      • 계산 효율이 좋아야 한다.

    • 활성화 함수로서 부적절한 함수들

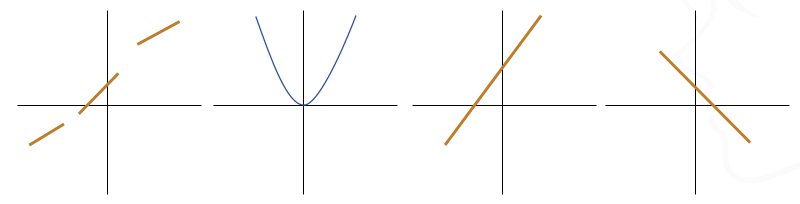
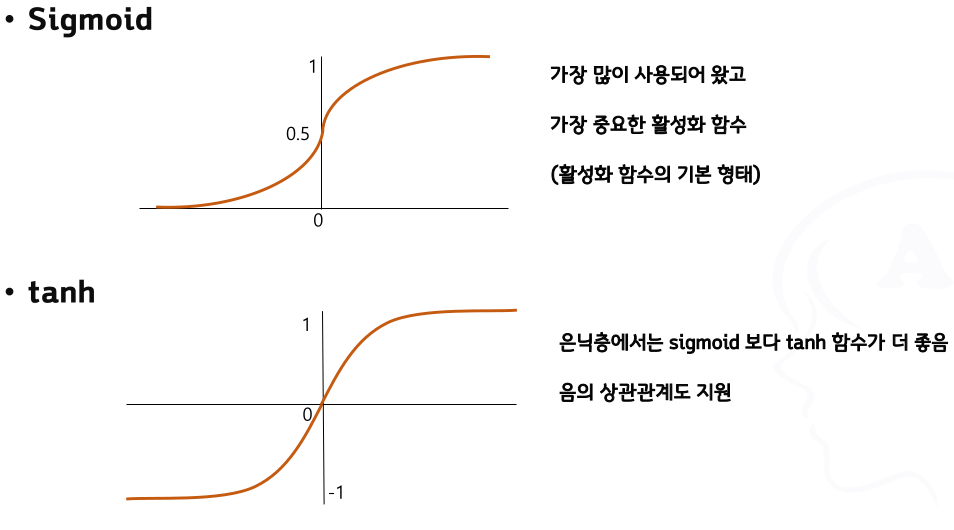
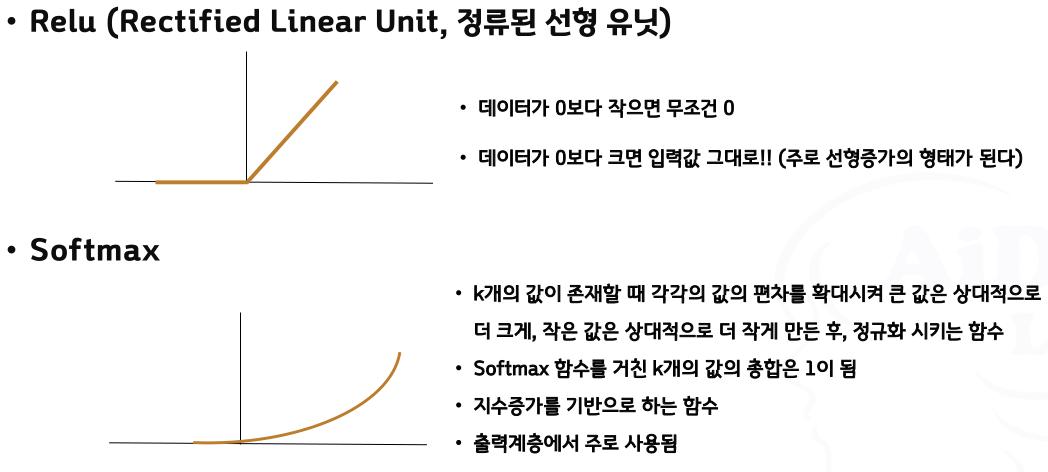
    • 활성화 함수의 종류





    • 표준 출력 계층 활성화 함수
      • 신경망의 목적에 따라 최선의 선택이 달라진다
        • 일반 데이터의 값 예측 ➜ 활성화 함수 미적용
        • 서로 무관한 항목에 대한 예/아니오 확률 예측 ➜ sigmoid
        • 여러 가능성 중 하나의 확률 예측 ➜ softmax
  • 오차의 측정
    • 출력층에서는 왜 오차를 측정하는가?
      • 신경망의 목적은 정확한 예측 결과를 얻는 것
        • 분류를 위한 모델은?
          • 분류 역시 어떤 클래스가 가장 잘 일치할 것인가를 예측, 계산하여 그 값이 가장 큰 것을 선택하는 것
      • 예측을 한 후에는 얼마나 잘 예측했는가 평가해야 함
        • 평가 방법으로 오차의 측정을 사용 ➜ 가장 간단하고 쉬운 방법이므로
      • 특히 가중치의 조정은 미분과 관련이 있다는 것은 오차의 값은 양수만 사용해야 한다는 의미
        • 미분은 거리, 넓이를 이용한 개념 ➜ 거리 또는 넓이는 음수가 없음
        • 실제로 오차를 측정하면 양수, 음수 모두 나올 수 있지만 각 값을 거리의 개념으로 바꿔서 사용
        • 절대값, 제곱 등을 이용하여 양수로 변환함
  • 손실 함수(Loss Function)
    • 출력 값과 정답(기대 값)의 오차를 정의하는 함수
    • 손실 함수는 데이터의 특성에 따라 변형, 새로 제안해서 사용 가능
    • 종류
      • 평균 제곱 오차 (MSE, Mean Squared Error)

        • 가장 많이 사용됨. 출력 값과 기대 값의 차이를 제곱하여 평균한 값
          \(MSE={\frac{1}{n}}\sum\limits_{i=1}^n (\widehat{Y_i}-Y_i)^2\)

        • 큰 오차는 더욱 크게, 작은 오차는 더욱 작게 ➜ 처리할 때에는 큰 오차에 더 집중(전반적인 성능 향상에 더 좋음)

      • 교차 엔트로피 오차 (Cross Entropy Error)
        • 범주형 데이터의 분류에 주로 사용
          \(CEE=-\sum\limits_{i=1}^n (Y_i \cdot log \widehat{Y_i})\)
    • 왜 손실함수를 사용하는가?
      • 학습의 궁극적인 목적은 높은 정확도를 끌어내는 매개변수를 찾는 것
      • 왜 “정확도”라는 지표를 놔두고 “손실함수의 값”이라는 우회적인 방법을 사용하는가?
      • 신경망 학습에서 미분의 역할을 생각해보면
        • 신경망 학습에서는 최적의 매개변수를 탐색할 때, 손실함수의 값을 가능한 작게 만드는 매개변수의 값을 찾음
        • 이때 매개변수의 미분을 계산하고, 그 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정을 반복함
          • 손실함수의 미분 값이 음수 → 가중치 매개변수를 양의 방향으로 변화시켜 손실함수의 값을 줄일 수 있다.
          • 손실함수의 미분 값이 양수 → 가중치 매개변수를 음의 방향으로 변화시켜 손실함수의 값을 줄일 수 있다.
          • 손실함수의 미분 값이 0 → 어느 쪽으로도 움직이지 않으므로 갱신이 멈춘다.
      • 정확도를 지표로 삼지 않는 이유
        • 정확도를 지표로 삼을 경우
          • 미분 값이 대부분의 장소에서 0이 되어 매개변수를 갱신할 수 없다.
          • 정확도는 매개변수의 작은 변화에는 거의 반응을 보이지 않거나, 갑자기 변화한다.
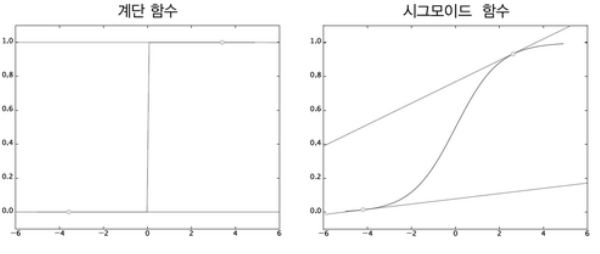
          • 활성화 함수로 ‘계단 함수’가 아닌 ‘시그모이드 함수’를 사용하는 이유도 같다.
        • 손실함수를 사용한다면
          • 계단함수는 대부분의 장소에서 기울기가 0 이지만, 시그모이드 함수의 기울기(접선)는 0이 아니다.
          • 계단 함수는 한순간만 변화를 일으키지만, 시그모이드 함수의 미분은 연속적으로 변한다.
          • 즉 시그모이드 함수의 미분은 어느 장소에서도 0이 되지 않는다.
          • 이는 신경망 학습에서 중요한 성질로, 기울기가 0이 되지 않는 덕분에 신경망이 올바르게 학습할 수 있다.
  • 가중치의 조정(=최적화, Optimizing)
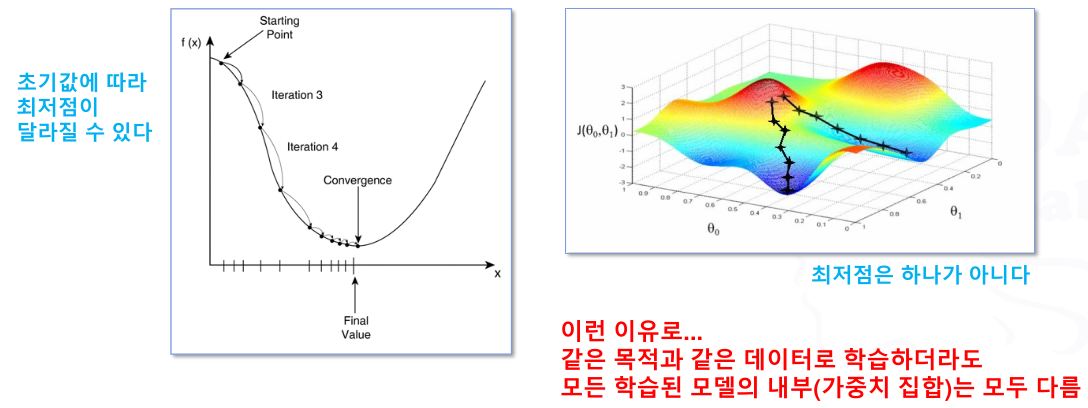
    • 경사 하강법 (Gradient Descent)
      • 가장 많이, 기본적으로 사용되는 가중치 조정 방법
    • 그 외의 가중치 조정 방법들..
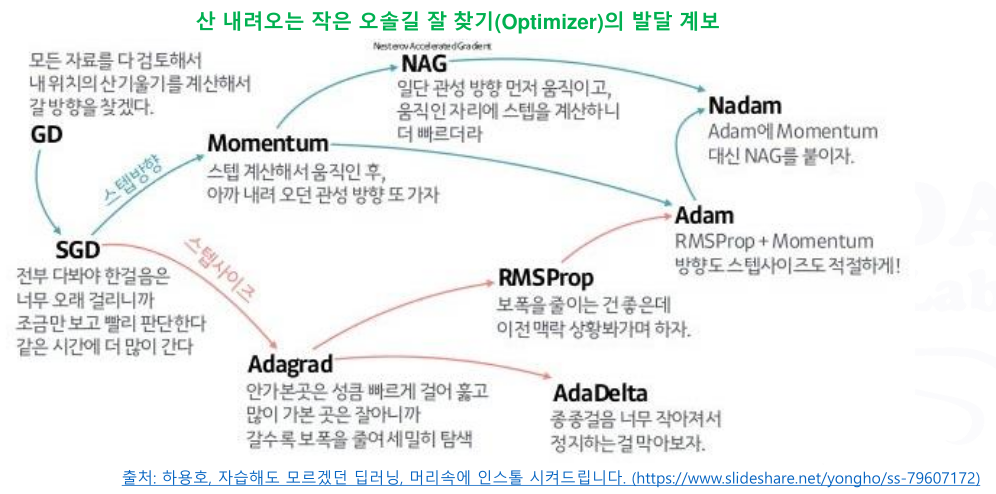
      • SGD, Momentum, AdaGrad, RMSprop, Adam 등

      • 다양한 가중치 조정 방법의 변화

    • 가중치 계산 방법으로 사용할 수 없는 것은?
      • 딥러닝 모델에서의 가중치 계산, 조정은 미분의 개념을 기반으로 움직임
      • 부드럽게 이어지지 않고 뾰족하거나 각진 형태로 인하여 미분이 불가능한 그래프의 형태를 가지는 계산 모델은 사용할 수 없음
  • 과적합(Overfitting)
    • 과적합의 개념
      • 주어진 데이터로 학습을 너무 많이 하면 오히려 역효과!!
        • 학습에 입력된 데이터는 완벽에 가깝게 처리함
        • 학습에 입력되지 않은 데이터는 제대로 처리되지 않음
    • 과적합의 원인: 잡음 데이터 (대부분)
      • 불필요한 정보가 많이 포함된 데이터로 학습이 반복됨에 따라 불필요한 정보가 분류의 기준에 포함되어 버리는 것이 원인
    • 과적합(Overfitting)의 해결 방안
      • 조기 종료
        • 적당한 선에서 학습을 종료시킴 → 데이터의 정규화와 관련
      • 정규화 (데이터를 일반화 시키기)
        • 필요한 신호는 학습하고 잡음은 제거하는 효과
        • 모델의 학습 난이도를 높임으로써 학습 데이터의 세부 사항(잡음 포함)에 대한 일반화를 활용하도록 하는 기법의 일부로 사용됨
      • Drop Out
        • 학습 중에 무작위로 선택한 뉴런을 0으로 설정 ➜ 군데군데 망의 연결고리를 잘라 내어 대형 신경망이 소형 신경망처럼 동작하게 만듦
        • 소형 신경망에서는 과적합이 거의 발생하지 않음 (표현능력이 협소하기 때문)
        • 대형 신경망(딥러닝 모델)을 Drop Out을 통해 소형 신경망처럼 동작하게 하여 과적합 발생률을 떨어뜨리는 방법
      • 앙상블(Ensemble)
        • 앙상블(Ensemble): 통일, 조화를 뜻하는 프랑스어. 음악에서 여러 악기들에 의한 협주를 의미함
          • 많은 수의 작은 악기소리가 조화를 이루어 더욱 더 웅장하고 아름다운 소리를 만들어 냄
          • 그런데 한 명의 아주 작은 실수는 다른 소리에 묻히기도 함
        • 기계학습에서의 앙상블: 많은 작은 모델이 모여 투표(Voting)를 통해 더욱 강력한 기능/결과를 도출함
          ➜ 많은 모델이 함께 동작하기 때문에 소수의 일부 모델에서 예측을 잘못하더라도 일정수준 보정됨
          ➜ 보다 일반화된 모델을 완성할 수 있음
        • 학습 방식에 따라 배깅(Bagging), 부스팅(Boosting), 스태킹(Stacking)으로 나눌 수 있음
          • 배깅(Bagging): Bootstrap Aggregating의 약자. 부트스트랩 (Boostrap)을 이용함. Random Forest 등
          • 부스팅(Boosting): 반복적으로 모델을 업데이트하면서 데이터셋 샘플에 대한 가중치를 부여함
          • 스태킹(Stacking): Weak learner들의 예측 결과를 바탕으로 meta learner로 학습시켜 최종 예측값을 결정함



  • 엄밀하게 따지면 딥러닝이란… 다수의 노드에 적용되는 최적화 프로그램이다.
  • 그렇다면 이것은 인공지능이 아니지 않나?
    • 애초에 인간의 두뇌 역시 다양한 입력의 결과를 올바르게 출력하기 위한 최적화 과정을 처리함
    • 많이 사용될 수록 굵어지고 민감해지는 각 신경세포 간의 시냅스 결합 강도를 뉴런 사이의 가중치로 모델링하여 구현한 것일 뿐!!